You may discover the intriguing implications of the equation Which Represents if X = 4, Then Y = −2”?
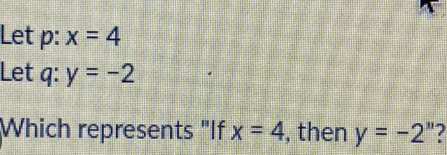
The statement “Which Represents if X = 4, Then Y = −2”? encapsulates a fundamental principle in mathematics, illustrating the nature of conditional relationships between variables. This specific correlation not only implies a fixed outcome when X assumes a particular value, but also invites further exploration into how such equations can be visualized and applied in various contexts. The implications of this relationship extend beyond mere numbers, raising questions about its utility in real-world scenarios and the broader mathematical frameworks that govern such interactions. What might these connections reveal about the equations we encounter daily?
Understanding Conditional Statements
Understanding conditional statements is essential for grasping the logical foundations of mathematical reasoning, as they establish relationships between hypotheses and conclusions in a precise manner.
Conditional logic facilitates the exploration of variable relationships, allowing for the deduction of outcomes based on specific conditions.
This clarity in reasoning empowers individuals to navigate complex scenarios, fostering analytical skills crucial for independent thought and decision-making.
See also A Comprehensive Guide:Wallpaper:Ynhkl56abmc= Panda
Graphical Representation of Variables
Graphical representation of variables serves as a vital tool in visualizing relationships and trends within data sets, enabling clearer interpretation of complex mathematical concepts.
By employing graphical patterns, one can effectively depict variable relationships, facilitating insights that may remain obscured in numerical form.
Such visualizations not only enhance comprehension but also empower individuals to explore and analyze data with greater freedom and understanding.
Real-World Applications of Equations
The insights gained from graphical representations of variables can be effectively applied in real-world scenarios, where equations serve as fundamental tools for modeling and solving complex problems across various fields such as physics, economics, and engineering.
In particular, predictive modeling utilizes equations for pattern recognition, while economic forecasting relies on mathematical frameworks to anticipate trends, providing valuable insights for decision-making processes.
See also Discover its Wallpaper:Xr5k797yocu= Marshmello unique features now!
Conclusion
In the realm of mathematics, conditional statements serve as guiding stars, illuminating the path between variables.
The relationship ‘if X = 4, then Y = -2’ exemplifies the clarity and precision inherent in mathematical reasoning.
By graphing this relationship, one can visualize the fixed point at (4, -2), reinforcing the predictability of Y in response to X.
Such equations not only enhance understanding but also underscore the importance of defined parameters in logical deduction and real-world applications.




