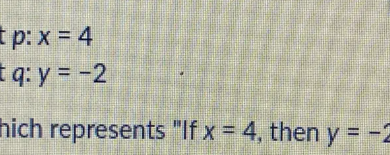Many intriguing mathematical Let P: X = 4 Let Q: Y = −2 Which Represents if X = 4, Then Y = −2”?
The conditional statement Let P: X = 4 Let Q: Y = −2 Which Represents if X = 4, Then Y = −2”? introduces a fundamental concept in mathematical logic, illustrating the dependency of one variable on another. Here, the assertion that Y equals -2 is contingent upon the specific value of X being 4, prompting a closer examination of how such relationships govern our understanding of variables. This interplay raises intriguing questions about the implications of conditional logic and its broader applications. What, then, might this suggest about the nature of relationships in more complex mathematical frameworks?
Understanding Conditional Statements
Conditional statements are fundamental constructs in logic that establish a relationship between two propositions, where the truth of one proposition depends on the truth of another.
These statements define conditional relationships, illustrating logical implications that guide reasoning.
See also Glimpse the future of anatomical understanding through the Labeled:T0fa22k6krs= Skeleton Diagram
The Significance of Variables
Variables serve as essential components in logical frameworks, allowing for the representation and manipulation of values that can influence the outcomes of various statements and propositions.
Through significance analysis, we can explore variable relationships, examining how changes in one variable impact another.
This understanding not only fosters clarity in logical reasoning but also equips individuals with tools for informed decision-making in diverse contexts.
Applications in Mathematical Logic
The relationships established through variables in logical frameworks find practical applications in mathematical logic, where they serve as the foundation for constructing and evaluating mathematical statements and proofs.
Truth tables are instrumental in assessing logical implication, illustrating how the truth of one statement can influence another.
This analytical approach enhances understanding, allowing for the rigorous exploration of logical relationships and their implications within mathematical systems.
See also Discover how the ‘Labeled:Uj3t4zt70_Q= Map of Us
Conclusion
In the realm of mathematical logic, the conditional statement ‘if X = 4, then Y = -2’ serves as a beacon illuminating the intricate interplay between variables.
This relationship, akin to a tightly woven tapestry, underscores the profound influence of one variable on another.
Understanding such dependencies is paramount, as they form the bedrock of logical reasoning.
Thus, the exploration of these conditional relationships enriches the comprehension of mathematical structures, revealing the symbiotic nature of variables within the mathematical landscape.